![[*]](crossref.png) beschrieben, in ein kartesisches System zu übertragen.
beschrieben, in ein kartesisches System zu übertragen.
Gegeben ist ein Straßenstück als Strecke ![]() . Die vom
GPS-Empfänger gemessene Position sein
. Die vom
GPS-Empfänger gemessene Position sein ![]() . Gesucht ist der Punkt
. Gesucht ist der Punkt ![]() auf
auf ![]() mit dem geringsten Abstand zu
mit dem geringsten Abstand zu ![]() .
. ![]() ist der Schnittpunkt
von AB mit der Senkrechten zu
ist der Schnittpunkt
von AB mit der Senkrechten zu ![]() durch
durch ![]() . Falls
. Falls ![]() zwischen
zwischen ![]() und
und ![]() liegt ist das der gesuchte Punkt
liegt ist das der gesuchte Punkt ![]() , ansonsten ist
, ansonsten ist ![]() als
der Endpunkt der Strecke zu wählen, der näher an
als
der Endpunkt der Strecke zu wählen, der näher an ![]() liegt. Zu Beginn
der Berechnung sind die Punkte, wie auf Seite
liegt. Zu Beginn
der Berechnung sind die Punkte, wie auf Seite ![[*]](crossref.png) beschrieben, in ein kartesisches System zu übertragen.
beschrieben, in ein kartesisches System zu übertragen.
Die Gerade ![]() durch
durch ![]() und
und ![]() lautet in Punkt-Richtungsform:
lautet in Punkt-Richtungsform:
| (5.1) |
Zur Bestimmung der Gerade ![]() durch P,
durch P, ![]() wird ein
Richtungsvektor
wird ein
Richtungsvektor ![]() senkrecht zur Richtung
senkrecht zur Richtung ![]() von
von ![]() benötigt.
benötigt.
| (5.2) | 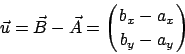 |
Der Vektor
![]() erfüllt
diese Bedingung, da
erfüllt
diese Bedingung, da
| (5.3) | 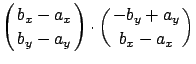 | ||
| (5.4) | |||
| (5.5) | |||
| (5.6) |
Damit lautet die Geradengleichung von g
| (5.7) |
Im Fußpunkt ![]() gilt:
gilt:
aus 5.8 folgt für
![]() :
:
| (5.10) |
| (5.11) | 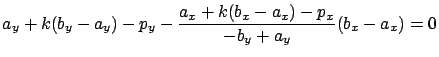 |
||
| (5.12) | 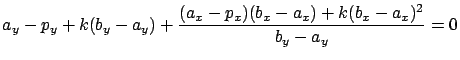 |
||
| (5.13) | 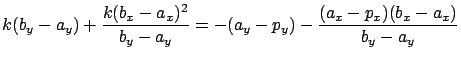 |
||
| (5.14) | 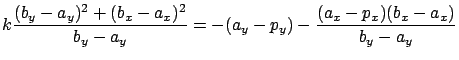 |
||
| (5.15) | |||
| (5.16) | 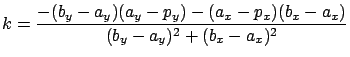 |
Das ![]() aus Gleichung 5.17 wird explizit berechnet, da es nicht nur
in Gleichung 5.18 zur Berechnung des Fußpunktes
aus Gleichung 5.17 wird explizit berechnet, da es nicht nur
in Gleichung 5.18 zur Berechnung des Fußpunktes ![]() benötigt wird.
Anhand von
benötigt wird.
Anhand von ![]() kann geprüft werden, ob sich
kann geprüft werden, ob sich ![]() auf
auf ![]() befindet.
Für
befindet.
Für
![]() liegt
liegt ![]() auf
auf ![]() . Für
. Für ![]() liegt
liegt ![]() außerhalb von
außerhalb von ![]() , näher bei
, näher bei ![]() und für
und für ![]() liegt
liegt ![]() außerhalb
von
außerhalb
von ![]() , näher bei
, näher bei ![]() .
.
Wenn die Straße parallel zur y-Achse verläuft, das heißt genau in Ost-West
bzw. West-Ost Richtung, dann ist ![]() . In diesem Fall ist
. In diesem Fall ist
| (5.19) | 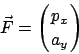 |
Falls der Abstand ![]() größer als der Abstand
größer als der Abstand
![]() ist, liegt
ist, liegt ![]() außerhalb von
außerhalb von ![]() , näher bei
, näher bei
![]() . Für
. Für
![]() liegt
liegt ![]() entsprechend
außerhalb, näher bei
entsprechend
außerhalb, näher bei ![]() . Ansonsten liegt
. Ansonsten liegt ![]() zwischen
zwischen ![]() und
und ![]() .
.
Falls ![]() nicht zwischen
nicht zwischen ![]() und
und ![]() liegt, wird der Endpunkt, der
näher an
liegt, wird der Endpunkt, der
näher an ![]() liegt als auf die Straße verbesserte Position
liegt als auf die Straße verbesserte Position ![]() verwendet.
Für
verwendet.
Für ![]() zwischen
zwischen ![]() und
und ![]() ist
ist ![]() .
.
Ein Straßenzug kann aus mehreren Geraden bestehen. Zu jeder Geraden
wird ein Punkt ![]() bestimmt. Derjenige Punkt mit dem kleinsten
Abstand
bestimmt. Derjenige Punkt mit dem kleinsten
Abstand
![]() ist die gesuchte Position auf der Straße mit
dem kleinsten Abstand von
ist die gesuchte Position auf der Straße mit
dem kleinsten Abstand von ![]() .
.